INTEGRALES DIRECTAS
Muchas veces se puede aplicar la relación dada en el teorema fundamental
del cálculo. Esto es cuando se conoce una función cuya derivada es
f(x), entonces la función es el resultado de la antiderivada. Este
método requiere del uso de las propiedades de las operaciones dado el
caso de la integral, como las propiedades de la potenciación, radicación
y demás operaciones primarias y secundarias. Este método de resolución
requiere una tabla de funciones y sus antiderivadas, estas se presentan a
continuación:
Un ejemplo de esto es:
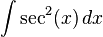 .
.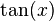 es
es  . Por tanto:
. Por tanto: 

No hay comentarios:
Publicar un comentario