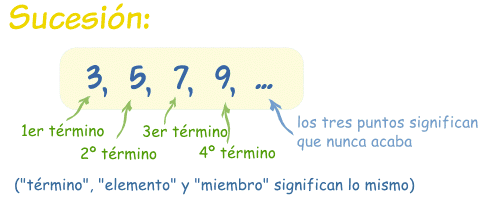
Una sucesión es un conjunto de cosas (normalmente números) una detrás de otra, en un cierto orden.
Finita o infinita
Si la sucesión sigue para siempre, es una sucesión infinita,
si no es una sucesión finita
Ejemplos
{1, 2, 3, 4 ,...} es una sucesión muy simple (y es una sucesión infinita)
{20, 25, 30, 35, ...} también es una sucesión infinita
{1, 3, 5, 7} es la sucesión de los 4 primeros números impares (y es una sucesión infinita)
{4, 3, 2, 1} va de 4 a 1 hacia atrás
{1, 2, 4, 8, 16, 32, ...} es una sucesión infinita donde vamos doblando cada término
{a, b, c, d, e} es la sucesión de las 5 primeras letras en order alfabético
{a, l, f, r, e, d, o} es la sucesión de las letras en el nombre "alfredo"
{0, 1, 0, 1, 0, 1, ...} es la sucesión que alterna 0s y 1s (sí, siguen un orden, en este caso un orden alternativo)
En orden
Cuando decimos que los términos están "en orden", ¡nosotros somos los que decimos qué orden! Podría ser adelante, atrás... o alternando... ¡o el que quieras!
Una sucesión es muy parecida a un
conjunto, pero con los términos
en orden (y el mismo valor sí puede aparecer muchas veces).
Ejemplo: {0, 1, 0, 1, 0, 1, ...} es la sucesión que alterna 0s y 1s. El conjunto sería sólo {0,1}
La regla
Una sucesión sigue una regla que te dice cómo calcular el valor de cada término.
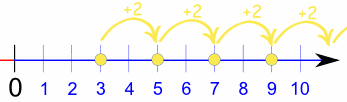
Ejemplo: la sucesión {3, 5, 7, 9, ...} empieza por 3 y salta 2 cada vez:
¡Pero la regla debería ser una fórmula!
Decir que "empieza por 3 y salta 2 cada vez" no nos dice cómo se calcula el:
- 10º término,
- 100º término, o
- n-ésimo término (donde n puede ser cualquier número positivo que queramos).
Así que queremos una fórmula con "n" dentro (donde n será la posición que tiene el término).
Entonces, ¿cuál sería la regla para {3, 5, 7, 9, ...}?
Primero, vemos que la sucesión sube 2 cada vez, así que podemos adivinar que la regla va a ser "2 × n". Vamos a verlo:
Probamos la regla: 2n
| n | Término | Prueba |
|---|
| 1 | 3 | 2n = 2×1 = 2 |
| 2 | 5 | 2n = 2×2 = 4 |
| 3 | 7 | 2n = 2×3 = 6 |
Esto casi funciona... pero la regla da todo el tiempo valores 1 unidad menos de lo que debería, así que vamos a cambiarla un poco:
Probamos la regla: 2n+1
| n | Término | Regla |
|---|
| 1 | 3 | 2n+1 = 2×1 + 1 = 3 |
| 2 | 5 | 2n+1 = 2×2 + 1 = 5 |
| 3 | 7 | 2n+1 = 2×3 + 1 = 7 |
¡Funciona!
Así que en vez de decir "empieza por 3 y salta 2 cada vez" escribimos la regla como
La regla para {3, 5, 7, 9, ...} es: 2n+1
Ahora, por ejemplo, podemos calcular el término 100º: 2 × 100 + 1 = 201
Notación
Para que sea más fácil escribir las reglas, normalmente lo hacemos así:
| |
Posición del término
|
 |
Es normal usar xn para los términos:
- xn es el término
- n es la posición de ese término
|
| | Así que para hablar del "quinto término" sólo tienes que escribir: x5 |
Entonces podemos escribir la regla para {3, 5, 7, 9, ...} en forma de ecuación, así:
xn = 2n+1
Ahora, si queremos calcular el 10º término, podemos escribir:
x10 = 2n+1 = 2×10+1 = 21
¿Puedes calcular el 50º término? ¿Y el 500º?
Ahora veamos algunas sucesiones especiales y sus reglas:
Tipos de sucesiones
Sucesiones aritméticas
El ejemplo que acabamos de usar, {3,5,7,9,...}, es una sucesión aritmética (o progresión aritmética), porquela diferencia entre un término y el siguiente es una constante.
Ejemplos
| 1, 4, 7, 10, 13, 16, 19, 22, 25, ... |
Esta sucesión tiene una diferencia de 3 entre cada dos términos.
La regla es xn = 3n-2
| 3, 8, 13, 18, 23, 28, 33, 38, ... |
Esta sucesión tiene una diferencia de 5 entre cada dos términos.
La regla es
xn = 5n-2
Sucesiones geométricas
En una sucesión geométrica cada término se calcula multiplicando el anterior por un número fijo.
Ejemplos:
| 2, 4, 8, 16, 32, 64, 128, 256, ... |
Esta sucesión tiene un factor 2 entre cada dos términos.
La regla es xn = 2n
| 3, 9, 27, 81, 243, 729, 2187, ... |
Esta sucesión tiene un factor 3 entre cada dos términos.
La regla es xn = 3n
Esta sucesión tiene un factor 0.5 (un medio) entre cada dos términos.
La regla es xn = 4 × 2-n
Sucesiones especiales
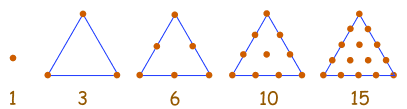
Números triangulares
| 1, 3, 6, 10, 15, 21, 28, 36, 45, ... |
Esta sucesión se genera a partir de una pauta de puntos en un triángulo.
Añadiendo otra fila de puntos y contando el total encontramos el siguiente número de la sucesión.
Pero es más fácil usar la regla
xn = n(n+1)/2
Ejemplo:
- El quinto número triangular es x5 = 5(5+1)/2 = 15,
- y el sexto es x6 = 6(6+1)/2 = 21
Números cuadrados
| 1, 4, 9, 16, 25, 36, 49, 64, 81, ... |
El siguiente número se calcula elevando al cuadrado su posición.
La regla es xn = n2
Números cúbicos
| 1, 8, 27, 64, 125, 216, 343, 512, 729, ... |
El siguiente número se calcula elevando al cubo su posición.
La regla es xn = n3
| 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, ... |
El siguiente número se calcula sumando los dos que están antes de él.
El 2 se calcula sumando los dos delante de él (1+1)
El 21 se calcula sumando los dos delante de él (8+13)
La regla es xn = xn-1 + xn-2
Esta regla es interesante porque depende de los valores de los términos anteriores.
Por ejemplo el 6º término se calcularía así:
x6 = x6-1 + x6-2 = x5 + x4 = 5 + 3 = 8
Series
"Sucesiones" y "series" pueden parecer la misma cosa... pero en realidad una serie es la suma de una sucesión.
Sucesión: {1,2,3,4}
Serie: 1+2+3+4 = 10
Las series se suelen escribir con el símbolo Σ que significa "súmalos todos":
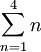 | Esto significa "suma de 1 a 4" = 10 |
| | |
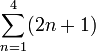 | Esto significa "suma los cuatro primeros términos de la sucesión 2n+1"
Que son los cuatro primeros términos de nuestro ejemplo {3,5,7,9,...} = 3+5+7+9 = 24 |


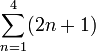






 . Aquí a = 0, b = 2, y1 = 0 y y2 = x3
. Aquí a = 0, b = 2, y1 = 0 y y2 = x3























 en el intervalo [0, 1].
en el intervalo [0, 1].





