FIGURAS AMORFAS:
Las figuras amorfas "son aquellas figuras que no tiene
forma”. Es una curva o una figura de muchos lados distintos. Su principal
finalidad es encontrar en una gráfica dada su área de la parte de adentro de una figura donde se
encuentra el punto dado de la figura amorfa.

Calcular las áreas de una figura regular es una tarea muy fácil, por lo cual la sustitución de la longitud, anchura u otras cantidades en la fórmula produciría el resultado.
Sin embargo, la estimación del área bajo la curva de las funciones no es tan sencilla ya que existen figuras amorfas y no fórmulas directas para estimaresta área.
La integración puede ser utilizada fructíferamente en una situación semejante.
Existen cuatro gráficas posibles para las cuales el área necesita ser evaluada.
Estas son: 1 Cuando el área está limitada por la curva y = f(x), el eje x y las ordenadas x = a y x = b.
El gráfico de la función se muestra a continuación,
Para estimar el área de tal figura, considereque el área bajo la curva estácompuesto por un gran número de delgadas tiras verticales.
Suponiendo que hay una tira arbitraria y para la altura y una dxpara la anchura. El área de esta tira elemental sería, dA = y dx donde y = f(x)
El área total A de la región entre el eje x, la ordenada x = a y x = b y la curva y = f (x) será la sumatoria de las áreas de todas las tiras elementales en toda la región o la zona limitada.
Esto produce la fórmula, A = dA = y dx = f(x) dx La integral anterior puede ser evaluada mediante poner la función en su lugar e integrándola.
2 La segunda situación es cuando el área está delimitada por la curva x = g(y), el eje y, y las ordenadas y = y1 y y2 = y. La gráfica de la función se muestra a continuación,
Asuma que el área bajo la curva está compuesta de un gran número de tiras delgadas horizontales. Sea una tira arbitraria dypara la altura y xpara la longitud. El área de esta tira elemental sería, dA = x dy donde x = g(y)
El área total A de la región entre el eje x, la ordenada y = y1 y y2 = y, y la curva x = g(y) será la sumatoria de las áreas de todas las tiras elementales en toda la región o el área limitada. Esto produce la fórmula, A = dA = x dy = g(y) dy
3 Se presenta una tercera situación cuando la curva en cuestión se encuentra por debajo del eje x, entonces f(x) es menor que cero desde x = a hasta x = b, el área limitada por la curva y = f(x) y las ordenadas x = a y x = b, y el eje x es negativo.
Pero el valor numérico del área debe ser tomado en consideración,entonces
A = | f(x) dx|
4 Una última posibilidad sería que una parte de la curva esté por encima del eje x y otra parte esté por debajo del eje x. Sea A1 el área debajo del eje x y A2 el área por encimadel eje x. Por lo tanto, el área limitada por la curva y = f(x), el eje x y las ordenadas x = a y x = b serán,
A = |A1| + A2
Tomemos ahora un ejemplo para entender la solución de tales problemas,
Encuentre el área de la región limitada por la curva y2 = x y las rectas x = 1, x = 4 y por el eje x.
La curva y2 = x es una parábola con su vértice en el origen. El eje de x es la línea de simetría la cual es el eje de la parábola.
NOTACIÓN SIGMA:
La sumatoria o sumatorio (llamada también notación sigma) es una operación matemática que se emplea para calcular la suma de muchos o infinitos sumando.
La operación sumatoria se expresa con la letra griega sigma mayúscula Σ, y se representa así:
Expresión que se lee: "sumatoria de Xi, donde i toma los valores desde 1 hasta n".
i es el valor inicial, llamado límite inferior.
n es el valor final, llamado límite superior.
Pero necesariamente debe cumplirse que:
i ≤ n
Si la sumatoria abarca la totalidad de los valores, entonces no se anotan sus límites y su expresión se puede simplificar:
Ahora, veamos un ejemplo:
Si se quiere expresar la suma de los cinco primeros números naturales se puede hacer de esta forma:
HISTORIA
La historia relata que cuando Carl Friedrich Gauss tenía diez años su profesor de matemática le impuso al curso, como una forma de mantenerlos ocupados por largo rato, el siguiente ejercicio:
Sumar todos los números desde el 1 hasta el 100, de este modo:
1 + 2+ 3 + 4 + 5 + 6 + 7 + 8 + 9 + ……………….+ 98 + 99 + 100 =
Confiado en que los niños estarían ocupados durante mucho rato, el profesor se enfrascó en sus tareas de estudio, pero a los cinco minutos, el pequeño Gauss le entregó el resultado: 5.050.
Sorprendido, el profesor le pidió a Gauss que le explicara cómo lo hizo:
El pequeño se dio cuenta de que la suma del primer número con el último (1 + 100 = 101) da un resultado que se repite sumando todos los simétricos: 1 + 100 = 101; 2 + 99 = 101; 3 + 98 = 101; 4 + 97 = 101; etc., logrando establecer 50 sumas cuyo resultado es 101.
Entonces, hizo: 50 veces 101 es igual a 50 x 101 = 5.050
Este procedimiento nos conduce a la fórmula de la sumatoria de n números consecutivos:
Si aplicamos la fórmula al problema anterior, tendremos:
Por ejemplo, para sumar los primeros mil números naturales no tiene mucho sentido sumar número por número, si se puede usar la fórmula:
FORMULAS DE NOTACIÓN SIGMA
Fórmula para la suma de n números consecutivos (1+ 2 + 3 + 4 + 5 ……+ n); que acabamos de ver arriba.
Fórmula para la sumatoria de los cuadrados de n números consecutivos (12 + 22 + 32 + 42 + 52 + 62 + ……….+ n2) :
Fórmula para la sumatoria de los cubos de n números consecutivos (13 + 23 + 33 + 43 + 53 + 63 + 73……..+ n3):
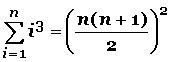
SUMA DE REIMANS
onsideremos lo siguiente:
- una función
![f:[D]\rightarrow\mathbb{R}](http://upload.wikimedia.org/math/2/9/3/293bb52f0a89d73cc4f24b6308e7471c.png)
- donde D es un subconjunto de los números reales

- I = [a, b] un intervalo cerrado contenido en D.
- Un conjunto finito de puntos {x0, x1, x2, ... xn} tales que a = x0 < x1 < x2 ... < xn = b
- crean una partición de I
- P = {[x0, x1), [x1, x2), ... [xn-1, xn]}
Si P es una partición con n elementos de I, entonces la suma de Riemann de f sobre I con la partición P se define como

- donde xi-1 ≤ yi ≤ xi. La elección de yi en este intervalo es arbitraria.
- Si yi = xi-1 para todo i, entonces denominamos S como la suma de Riemann por la izquierda.
- Si yi = xi, entonces denominamos S como la suma de Riemann por la derecha.
Suma Trapezoidal
-
-
En este caso, el valor de la función f en un intervalo se aproxima por el promedio de los valores de los extremos a izquierda y derecha. De la manera ya descripta, un simple cálculo usando la fórmula del área

para un trapecio con lados paralelos b1, b2 y altura h produces
![\tfrac{1}{2}Q\left[f(a) + 2f(a+Q) + 2f(a+2Q) + 2f(a+3Q)+\cdots+f(b)\right].](http://upload.wikimedia.org/math/6/c/6/6c6f88a63104ec42166e25fec072c394.png)
El error de esta fórmula será

donde

es el valor máximo del valor absoluto de

La aproximación obtenida con la
suma trapezoidal para una función es igual al promedio de las sumas izquierda y derecha de Riemann.





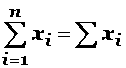
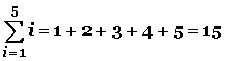
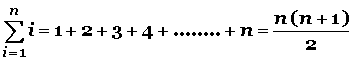
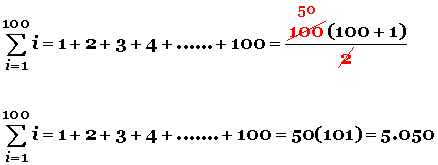
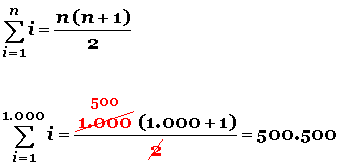
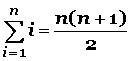
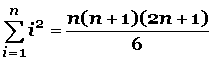
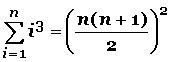
![f:[D]\rightarrow\mathbb{R}](http://upload.wikimedia.org/math/2/9/3/293bb52f0a89d73cc4f24b6308e7471c.png)



![\tfrac{1}{2}Q\left[f(a) + 2f(a+Q) + 2f(a+2Q) + 2f(a+3Q)+\cdots+f(b)\right].](http://upload.wikimedia.org/math/6/c/6/6c6f88a63104ec42166e25fec072c394.png)

 es el valor máximo del valor absoluto de
es el valor máximo del valor absoluto de 
